Il modello per la corda
 

Il modello di Karplus-Strong può essere preso come elemento di partenza da cui derivare un modello di corda efficiente.
Ad ampliare il modello base della guida d’onda digitale per la sintesi di strumenti a corde pizzicate sono state proposte molte strutture e implementazioni, come ad esempio l’utilizzo di interpolatori di Lagrange per un’accordatura più accurata della guida d’onda, e realizzare glissandi (Karjalainen e Laine, 1991), tecniche di filtraggio passatutto per simulare la dispersione causata dalla rigidità della corda.
 

Dalla guida d’onda digitale al modello ad anello con singolo ritardo.

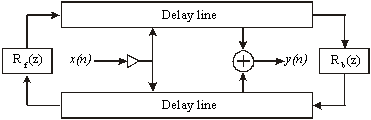
Il modello con guida d’onda digitale della corda proposto da Smith (Fig.5),

Fig.5

le due linee di ritardo possono essere interpretate come le soluzioni digitalizzate dell’equazione d’onda in una dimensione senza perdite. I due filtri R_f(z) e R_b(z) scaturiscono delle terminazioni rigide della corda e producono un’inversione di fase e un leggero smorzamento dipendente dalla frequenza. Nel modello di corda mostrato figura possono essere utilizzata come variabile d’onda velocità, accelerazione, posizione, pendenza o disposizione.Utilizzando l’accelerazione come variabile d’onda, l’eccitazione ideale della corda corrisponde all’impulso unitario (Smith 1983).

Si può dimostrare che il modello "più fisico " della guida d’onda digitale può essere ricondotto ad un modello con anello di ritardo singolo "SDL" (Karjalainen 98) che risulta una forma estesa dell’algoritmo di Karplus-Strong.

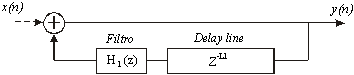
Fig.6

Il passaggio dalla doppia linea di ritardo al modello SDL, nel caso lineare e tempo invariante (LTI) risulta computazionalmente più efficiente. Per giungere ad un modello per la chitarra acustica, consideriamo il modello con guida d’onda per la corda pizzicata, si osserva che l’uscita del segnale è prelevata al ponte ovvero da una terminazione della corda. Sotto l’ipotesi che il sistema sia lineare e tempo invariante, rispettando il teorema del campionamento, è possibile passare alla rappresentazione dei vari blocchi funzionali nel dominio della trasformata Z.

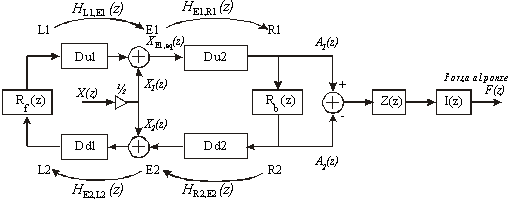
Fig.7

L’eccitazione equivalente al punto E1

.

Il segnale d’uscita è la forza risultante al ponte, può essere espressa come

rappresentando con H_E(z) la funzione di trasferimento equivalente della eccitazione.

l’eccitazione equivalente al punto E₁

X_E1,eq=H_E(z)X(z)

Il segnale d’uscita è la forza traversa al ponte F(z)

F(z)=F₊(z)+F_-(z)=Z(z)[V₊(z)-V_-(z)]=

=Z(z)[A₁(z)-A₂(z)]I(z)

dove ₊ o _– indicano la direzione di propagazione, Z(z) l’impedenza al ponte, V± (z) le componenti della velocità della corda al ponte, I(z) rappresenta un integratore ideale.

Indicando con H_B(z) la funzione di trasferimento da accelerazione a velocità al ponte

F(z)=Z(z)[A₁(z)-A₂(z)]I(z)=Z(z)[A₁(z)-R_b(z)A₁(z)]I(z)=
=Z(z)[1-R_b(z)I(z)]A₁(z)=H_B(z)A₁(z)

Per il segnale accelerazione A₁(z) vale la relazione

A₁(z)=H_E1,R1(z)X_E1,eq(z)+H_Loop(z)A₁

Dove H_Loop indica la funzione di trasferimento ad anello aperto della corda.

H_Loop(z)=R_b(z)H_R2,E2(z)H_E2,E1(z)H_E1,R1(z)

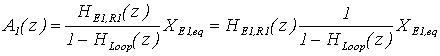
definendo S(z) la funzione di trasferimento della corda .

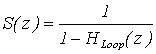
A₁(z)=H_E1,R1(z)S(z)X_E1,eq(z)

F(z)=H_E,B(z)X(z)

la funzione di trasferimento dall’eccitazione al ponte

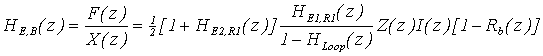
H_E,B(z)=H_E(z)H_E1,R1(z)S(z)H_B(z)

Il sistema complessivo H_E,B(z) può essere schematizzato come composto da quattro elementi.

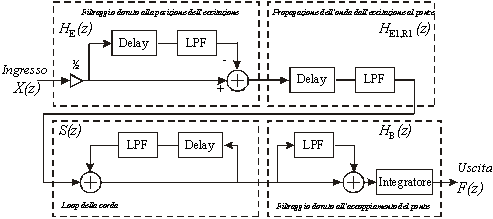
Fig.8

H_E(z) include il filtraggio dovuto alla posizione fisica dell’eccitazione, e vale

H_E1,R1(z) propagazione dell’onda dall’eccitazione al ponte, S(z) funzione di trasferimento della corda, H_B(z) filtraggio dovuto all’accoppiamento del ponte.

Una semplificazione del modello precedente può essere ottenuta considerando che:
In H_E(z), la funzione di trasferimento H_E2,E1(z) è composta da una linea di ritardo e da un filtro R_f(z), preservando la qualità della sintesi, è possibile cumulare il filtro passa basso nel filtraggio dell’eccitazione, inoltre la funzione di trasferimento da E1 a R1, composta da puro ritardo posto in serie ad un passa basso, può essere eliminata senza influenzare la sintesi. Infine, il termine [1-R_b(z)] presente in H_B(z) può essere semplificato con la costante 2, dato che R_b(z)@ -1.
Per compensare le semplificazioni introdotte, si può fare ricorso ad un’equalizzazione sul segnale d’ingresso. In figura è mostrato il modello semplificato.

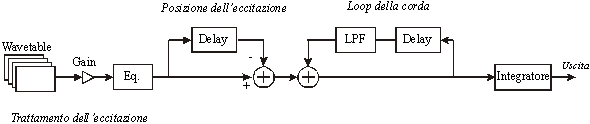
Fig.9

Il controllo sulla posizione dell’eccitazione è un filtro a pettine (comb filter), e il ritardo che lo caratterizza, corrisponde al tempo che l’eccitazione impiega a percorrere da E2 a E1. L’integratore al ponte può essere approssimato da un filtro passa basso del primo ordine, con una frequenza di taglio più bassa della fondamentale da sintetizzare. La funzione di trasferimento della corda S(z), non può essere semplificato, in quanto incide pesantemente sulla qualità della sintesi, essa può essere espressa come:

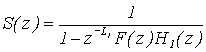
dove L₁ è la parte intera della lunghezza della corda,

H(z)  è chiamato loop filter, e F(z) è un filtro di ritardo frazionato, utilizzato per raffinare l’accordatura della corda.
I parametri che determinano la f.d.t. S(z), sono L₁ lunghezza della linea di ritardo, g e a, che sono rispettivamente guadagno e parametro di cutoff del loop filter.
 

Filtri a guida d’onda con ritardo frazionato

Teoricamente nei circuiti a tempo discreto, il ritardo unitario frazionato indica un elemento che ripropone in uscita ciò che aveva all’ingresso, dopo un ritardo pari a un multiplo non intero del intervallo di campionamento.

Dato che nella realizzazione pratica di algoritmi è sconveniente o impossibile realizzare un frazionamento dell’intervallo di campionamento; si può ricorrere all’uso di interpolatori, che offrono una stima del ritardo non intero.

Per estendere il modello a guida d’onda della corda si può utilizzare un interpolatore polinomiale, tale circuito in funzione di un parametro accessibile dal esterno, si comporta da elemento di ritardo non intero; realizza una stima del valore d’ingresso ritardato di un intervallo di tempo arbitrario, sulla base dei valori presenti e passati all’ingresso.

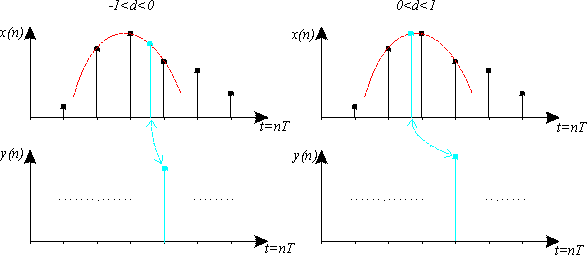
Fig.10

La stima essendo affetta da incertezza, introduce un degrado sul segnale che attraversa il ritardo frazionato. Si può dimostrare che l’errore introdotto dalla stima decresce all’aumentare del ordine dell’interpolatore, per contro la complessità circuitale e il costo computazionale tendono ad aumentare.
Un buon compromesso utilizzato nella realizzazione del circuito, è offerto da interpolatore del secondo ordine, riportato in figura 11.
Il ritardo tra ingresso e uscita può essere continuamente modificato agendo sul parametro t, secondo la funzione

si può facilmente verificare che

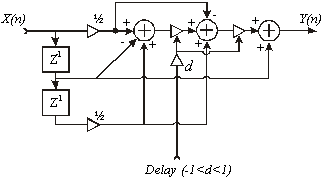
Fig.11

Nel modello di chitarra acustica realizzato, il ritardo frazionato è utilizzato come estensione delle linee di ritardo delle due polarizzazioni, oltre a permettere un’intonazione accurata della corda, offre la possibilità di agire in ogni istante sulla nota prodotta. Ad esempio, il tiraggio "bending" della corda può essere implementato semplicemente facendo assumere a t un valore crescente nel tempo.

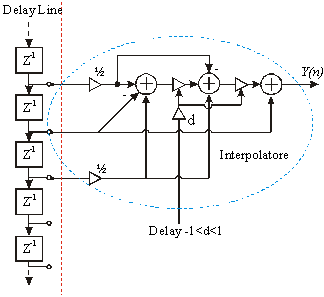
Fig.12

La struttura definitiva di linea di ritardo utilizzata è quella riportata in figura; in essa l’interpolatore è "fuso" con la linea di ritardo, così che reso privo di elementi di memoria, può essere spostato, indipendentemente dal tempo, lungo la linea di ritardo.
Nel contesto della sintesi di modelli, per le non linearità dipendenti dal segnale, il ritardo frazionato è stato proposto per la realizzazione di filtri non lineari (Valimaki, Tolonen e Karjalainen Icmc 1998).

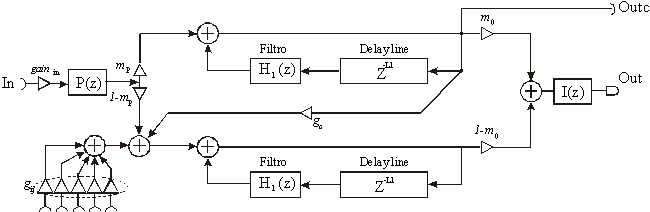
Fig.13

Il modello utilizzato per una singola corda è riportato in figura, ogni polarizzazione è composta da una linea di ritardo frazionata e dal rispettivo filtro, l’ingresso dopo la moltiplicazione per costante gain_in, passa all’ingresso del filtro a pettine P(z), con il quale è possibile variare la posizione "fisica" dell’eccitazione. Variando il parametro m_p è possibile ripartire il segnale d’ingresso sulle le due polarizzazioni, allo stesso modo il parametro m_o ne determina il contributo a formare il segnale d’uscita.

L’integratore per l’uscita al ponte I(z), può essere ben approssimato da un filtro passa basso del primo ordine con una frequenza di taglio più bassa alla fondamentale che deve essere sintetizzata.

Riguardo l’accoppiamento, g_c lo stabilisce tra le due polarizzazioni della stessa corda, e i parametri g_1i, g_2i, g_3i, g_4i e g_5i, moltiplicando i segnali provenienti dalle restanti corde, lo realizza con le altre corde.

______________________________

Pagina iniziale