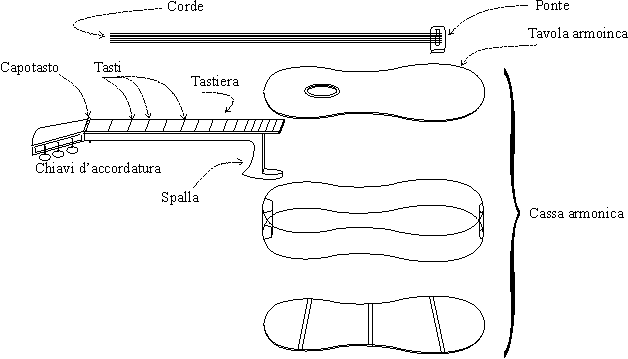
Il modello della chitarra
acustica
Il modello della corda con singola linea di ritardo può costituire l’elemento base con cui costruire un modello per lo strumento musicale, quale in questo caso la chitarra acustica. Come sistema acustico la chitarra, in prima analisi può essere suddivisa in due parti, la prima composta dalle corde (sei o dodici) ovvero l’elemento risonante, e la seconda la cassa acustica che costituisce l’elemento risonatore; questi due sistemi interagenti tra loro caratterizzano il timbro proprio dello strumento.

Fig.14
In figura 14 è riportato un esploso di una chitarra acustica.
Il contributo principale nel suono radiato
prodotto dalla chitarra è portato dalla tavola superiore della
cassa acustica, e definisce così la tavola armonica dello
strumento. A contatto con la tavola armonica, il ponte ne
permette la giunzione con le corde.
In una chitarra acustica i fenomeni significativi
d’accoppiamento sono, l’accoppiamento
d’intercorda, tra le due polarizzazione di una stessa corda,
e l’accoppiamento tra le corde e le risonanze del corpo. Una
soluzione proposta da Smith (1993), utilizza un filtro
d’accoppiamento al ponte, in quanto è condiviso da tutte e
sei le corde, il modello che a cui si perviene è fisicamente
corretto ma praticamente incorre in problemi di stabilità. Il
modello proposto da Karjalainen(1998) include fenomeni di
accoppiamento tra le corde, e tra le due polarizzazione di una
stessa corda, e risulta incondizionatamente stabile.
La simulazione di una corda col semplice modello SDL è poco
realistica, in quanto nasce come modello di una corda nel caso
monodimensionale.
Dato che la corda di chitarra reale vibra in due polarizzazioni
trasversali, per realizzare il modello bidimensionale di corda si
può ricorrere al utilizzo di due modelli di corda
monodimensionale posti in parallelo.
I due modelli di corda Sh(z) e Sv(z),
realizzano le due polarizzazioni trasversali.
La corda di chitarra reale non vibra uniformemente nelle due polarizzazione, questo fenomeno è dovuto principalmente al fatto che l’impedenza del ponte non è uniforme nelle due direzioni dei due piani di polarizzazione. Il battimento causato dalle due polarizzazioni della vibrazione della corda può essere realizzato sommando l’uscita di due modelli di corda monodimensionale. Se le due polarizzazioni sono leggermente "stonate" tra loro (fondamentali vicine), si produce l’effetto del battimento .
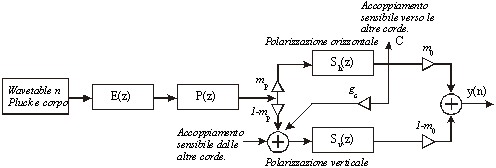
Fig.15
L’interazione tra le due polarizzazioni nel caso reale
avviene in modo bidirezionale, e in quantità dipendentemente
dalla frequenza; al fine di semplificare il modello senza
compromettere la qualità della sintesi è possibile concentrare
in un unico parametro costante gc
l’accoppiamento tra le due polarizzazioni. Si può osservare
che il modello di corda reale derivato non ha problemi di
stabilità.
Accoppiamento sensibile tra le corde
Per una generica corda l’eccitazione per le
vibrazioni sensibili verso le altre, è presa da una delle due
SDL che ne realizzano le polarizzazioni. Per evitare retroazioni,
l’ingresso dalle altre corde è sommato all’ingresso
delle corde che non hanno uscita d’accoppiamento sensibile.
I parametri che quantificano gli accoppiamenti nel modello di
Karjalainen possono essere racchiusi in forma matriciale.
Matrice di coefficienti d’accoppiamento C
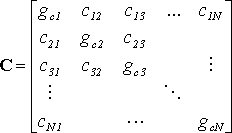
dove N è il numero delle corde a due polarizzazioni, i
coefficienti gck (per k =1,2…N) rappresentano
i guadagni del segnale d’uscita mandato dalla k-esima corda
orizzontale alla relativa corda verticale, e i coefficienti cmk
sono i guadagni dall’uscita della k-esima
polarizzazione orizzontale diretti all’ingresso della m-esima
polarizzazione verticale.
I parametri del modello
Variando liberamente i parametri, il modello sintetizza un
suono caratteristico delle corde. Volendo riprodurre fedelmente
il suono di una chitarra acustica, è necessario che i parametri
modello siano calibrati sperimentalmente, in quanto occupano il
ruolo principale nella qualità della sintesi. Dal sistema
possono essere messi in evidenza tre insiemi di parametri: i
parametri del modello della corda, i parametri del corpo
risonante e il segnale d’eccitazione.
La procedura per calibrare i parametri del modello e il segnale
d’eccitazione presentata da Tolonen e Valimaki
(FINSING’97, ISMA’97), utilizza registrazioni del suono
reale dello strumento acustico. La procedura d’estrazione è
divisa in tre parti, nella prima sono stimati i parametri della
corda, successivamente il segnale d’eccitazione è ottenuto
cancellando i parziali e le risonanze del corpo più basse,
sottraendo un modello sinusoidale del segnale originale, infine i
parametri per i risonatori del corpo separati sono ottenuti
analizzando il modello sinusoidale delle risonanze del corpo.
Tecniche di modellizzazione del corpo
La realizzazione di un filtro con la stessa risposta impulsiva del corpo dello strumento è teoricamente corretta ma praticamente svantaggiosa, a questo problema sono state proposte diverse soluzioni; Le tecniche più valide si basano sulla sintesi in guida d’onda commutata (CWS Commuted Waveguide Syntesis).
Dalla sintesi commutata, un modo efficiente di
realizzare le risonanze del corpo dello strumento, è quello di
riportarne la risposta impulsiva all’ingresso del modello, e
dopo la convoluzione con l’eccitazione, formare un segnale
d’eccitazione equivalente, memorizzabile in una tabella. Il
segnale prodotto ha durata di circa 100ms, equivalentemente
qualche migliaio di campioni in funzione della frequenza di
campionamento; Una realizzazione pratica basata su questa tecnica
prevede l’utilizzo di una tavola (Wavetable) dove
memorizzare i diversi tipi di eccitazione, quali potrebbero
essere ad esempio i diversi modi di colpire la corda; oltre a
richiedere memoria l’utilizzo di wavetable ha lo svantaggio
di offrire uno scarso controllo parametrico sul modello. Per
rendere più efficiente l’uso della sintesi commutata, si
può ricorrere all’estrazione delle risonanze del corpo più
basse. Le due componenti che caratterizzano la durata della
risposta impulsiva del corpo, sono la risonanza di Helmotz circa
100Hz ed il primo modo della tavola armonica circa 200Hz
(Karjalainen-Smith ICMC’96). Un segnale d’eccitazione
più breve può essere ottenuto dalla sottrazione nel dominio del
tempo delle due componenti principali dalla risposta impulsiva.
Le risonanze possono essere riprodotte nella sintesi da
risonatori del secondo ordine, inoltre offrono un maggiore
controllo parametrico sul segnale d’eccitazione.
Questa tecnica può essere migliorata in termini di costo
computazionale, introducendo un estensione multirate del modello
(Valimaki Tolonen Icmc1997), che propone per le due risonanze del
corpo, l’utilizzo di risonatori a bassa frequenza
interpolati (ILFRs) che operano a una frequenza inferiore a
quella del sistema.