Sintesi con guida d’onda digitale
 

Tra i vari metodi utilizzati per la modellizzazione fisica, quali: metodi alle differenze finite, modellizzazione Sorgente-Filtro, reti vibranti massa-molla, sintesi modale; la sintesi con guida d’onda digitale è uno dei più usati metodi di sintesi sonora su basi fisiche.

La sintesi con guida d’onda digitale è efficiente nella simulazione della propagazione dell’onda in sistemi vibranti omogenei monodimensionali. Le onde che si propagano sono esplicitamente simulate nel modello a guida d’onda, sommate insieme, producono l’uscita fisica. Nel caso privo di perdite le onde che si propagano tra due punti nel mezzo possono essere simulate utilizzando una linea di ritardo digitale. Nel caso lineare utilizzando la proprietà commutativa dei sistemi lineari tempo invarianti, si può facilmente trattare perdite dipendenti dalla frequenza e dispersioni, concentrandole in pochi punti, ottenendo cosi semplici linee di ritardo; ne consegue che la tecnica della guida d’onda digitale ha nella semplicità computazionale il principale punto di forza.

Teoria della guida d’onda digitale

L’equazione d’onda per una corda ideale, ovvero senza perdite, lineare, flessibile è espressa dalla relazione

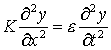
dove y è la disposizione della corda, x è la distanza dall’origine lungo la direzione della corda, t è il tempo, K è la tensione della corda, e è la densità di massa lineare.

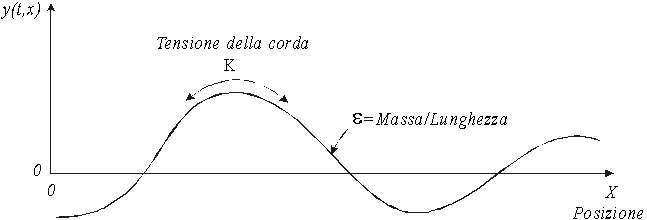
Fig .1

Si può dimostrare che l’equazione è soddisfatta da funzioni arbitrarie del tipo

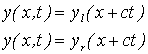
dove c è la velocità di propagazione pari a:

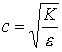
a condizione che y_l(x+ct) e y_r(x-ct) siano differenzialbili in x e t.
Un’interpretazione delle funzioni y_l(x+ct) e y_r(x-ct) può essere quella di onda progressiva (verso destra), e di onda regressiva (verso sinistra). La combinazione lineare delle due onde fornisce la soluzione generale per l’equazione d’onda. L’impiego della guida d’onda digitale implementa una discretizzazione delle funzioni y_l(x+ct) e y_r(x-ct), ottenuta dal cambiamento di variabili (Smith, 1993)

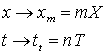
dove T è il periodo di campionamento, X è il corrispondente intervallo nello spazio, ed m ed n sono indici interi. Per le variabili così ottenute vale la relazione

La sostituzione di variabili nella soluzione dell’equazione d’onda produce

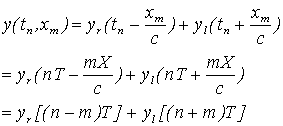
Dato che T moltiplica tutti gli argomenti, definendo

Si ottiene

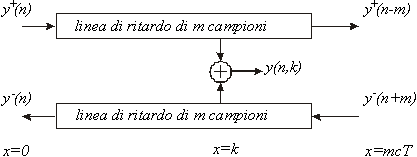
Fig .2

Le due funzioni discrete y⁺(n-m) e y^-(n-m) possono essere interpretate come linee di ritardo di m campioni (Smith 1992). Sommando le variabili al punto k della linea di ritardo si ottiene l’uscita dalla guida d’onda. La soluzione all’equazione d’onda mono-dimensionale data dalla guida d’onda è esatta nei punti discreti della linea di ritardo, o equivalentemente nel tempo negli istanti di campionamento, ma necessariamente le frequenze più alte presenti nei segnali y_r(t) e y_l(t), non devono superare la metà della frequenza di campionamento. Per stimare il valore delle variabili nella guida in punti non interi, è possibile utilizzare un interpolatore.
 

DWG con Dispersione e Smorzamento dipendente dalla frequenza.

L’equazione d’onda che descrive il movimento vibratorio della corda rigida che include: perdite dipendenti dalla frequenza dovute all’attrito con l’aria, alla viscosità e alla massa finita della corda può essere scrittta come (Smith, 1995)

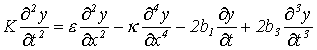
dove y è la disposizione della corda, x l’asse lungo la corda, b₁ e b₂ parametri di perdita. K e e sono la tensione della corda e la densità di massa lineare. Il parametro k è dato dalla relazione (Smith, 1992)

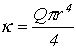
dove r è il raggio della sezione della corda, e Q è il modulo di Young.

La generalizzazione del caso lineare, tempo invariante dell’equazione d’onda per corde rigide con perdite è descritta da Smith (1995).

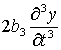Nell’equazione i termini  e  tengono conto delle perdite dipendenti dalla frequenza.

Nella soluzione d’onda le perdite dipendenti dalla frequenza fanno in modo che i fronti d’onda siano attenuati esponenzialmente nel tempo, in altri termini, le onde che si propagano, sono moltiplicate ad ogni passo per una costante dipendente dalla frequenza.

Indicando con G(w ) il fattore che determina la dipendenza dell’attenuazione in funzione della frequenza, ad ogni passo di tempo (Smith 1987,1992). Nella struttura della guida d’onda il fattore G(w ) deve essere inserito tra ogni unità di ritardo. Dato che il sistema è lineare e tempo invariante, in ogni sezione inosservata della guida è possibile concentrare i contributi dei vari G(w ).

Il termine tiene conto del fatto che la velocità delle onde dipendono dalla frequenza. Si può vedere dall’equazione, che tale termine è non nullo per corde con una rigidità finita (Q diverso da zero).

L’approssimazione al primo ordine della velocità dipendente dalla frequenza può essere espressa come (Smith 1992)

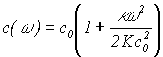
dove c₀ è la velocità della corda ideale e w è proporzionale alla frequenza. Dalla relazione si può osservare che le componenti di segnale di frequenza più elevata hanno velocità maggiore rispetto a quelle con frequenza più bassa. Quindi la forma della forma d’onda cambia nel tempo. Questo fenomeno è presente in ogni corda reale ed è chiamato dispersione. La dispersione può essere considerata nel modello della guida d’onda inserendo un filtro passa tutto prima di ogni punto d’osservazione. Van Duyne and Smith (1994).
 

La Corda vincolata

Supponendo una corda ideale di lunghezza L, bloccata alle estremità, quindi per x=0 e x=L, si ottengono le rispettive condizioni al contorno

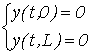
Dato che y(t,0)=y_r(t)+y_l(t)=y⁺(t/T)+ y^-(t/T) e y(t,L)=y_r(t-L/c)+y_l(t+L/c),
Il vincolo sulle onde campionate diventa

dove N=2L/X è definito come il tempo in campioni per la propagazione nei due sensi, da un capo all’altro della corda, oppure il ritardo totale del loop della corda.
In figura è mostrato il caso di una corda ideale terminata, l’uscita fisica è presa in un qualsiasi punto x=x .

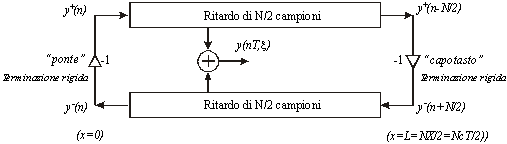
Fig3

La terminazione rigida riflette il segnale che si propaga, la velocità o l’accelerazione con un inversione di segno, nel caso di variabili onde di forza o posizione la riflessione è senza l’inversione di segno (Smith 1992).
 
 

Sintesi commutata

Nella sintesi commutata in guida d’onda "CWS" il modello dello strumento è suddiviso in tre parti l’eccitazione, la corda vibrante e il corpo radiante; considerate questi elementi come filtri lineari con funzioni di trasferimento, rispettivamente E(z), S(z) e B(z). Il sistema risultante all’ingresso è eccitato da un impulso d (n), conseguentemente all’ipotesi di linearità dei vari sottosistemi, il segnale d’uscita y(n), è ottenuto dalla convoluzione della risposta impulsiva dei tre filtri e(n), s(n) e b(n) con l’impulso unitario d (n), ovvero

nel dominio della trasformata Z, la relazione è espressa come

Sfruttando la proprietà commutativa per i sistemi lineari, si può riscrivere la relazione come

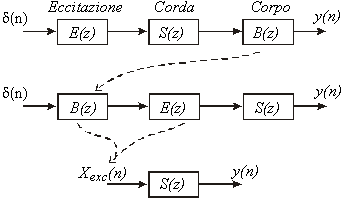
Fig.4

Questa relazione mette in evidenza la possibilità di convoluire le risposte impulsive del corpo e dell’eccitazione in una singola risposta impulsiva X_exc(n), da utilizzare come eccitazione al ingresso di S(z) per produrre lo stesso segnale d’uscita y(n). L’utilizzo di un’eccitazione equivalente è praticamente molto conveniente in quanto può essere precalcolato ed immagazzinato in una wavetable.

______________________________